
2.5角平分线的性质

(1)角是轴对称图形吗?如果是,请操作回答:
请你在纸上画出任意一个∠BAC,如何找出
它的对称轴?


再打开纸片 ,看看折
痕是哪一条直线?
(对折)


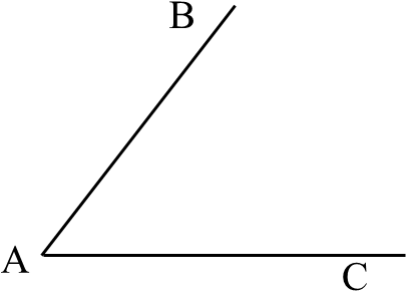

(2)如图,在∠BAC的角平分线上任意取一点P,
过点P作PM⊥AB,PN ⊥ AC,垂足分别是点M,N,
用圆规比较PM与PN的大小,你有什么发现?由此
可以得出什么结论?说明你的理由.

角平分线的性质:
角的平分线上的点到角的两边的距离相等.

你能用以前所学的知识加以推理说明吗?

探究角平分线的性质
证明:∵OC平分∠ AOB (已知)
∴ ∠1= ∠2(角平分线的定义)
∵PD ⊥ OA,PE ⊥ OB(已知)
∴ ∠PDO= ∠PEO(垂直的定义)
在△PDO和△PEO中
∠PDO= ∠PEO(已证)
∠1= ∠2 (已证)
OP=OP (公共边)
∴ △PDO ≌ △PEO(AAS)
∴PD=PE(全等三角形的对应边相等)

已知:如图,OC平分∠AOB,点P在OC
上,PD⊥OA于点D,PE⊥OB于点E
求证:PD=PE

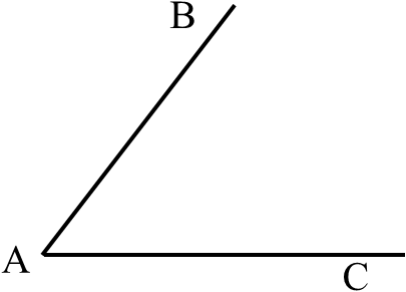
(3)如图,已知∠BAC,经过∠BAC内部任意作直线
l1∥AB,作直线l2∥AC,使得l2与AC之间的距离等于l1与
AB之间的距离.记l1 、l2的交点为P,则P是∠BAC内部一
个到∠BAC的两边AB、AC距离相等的点.作直线AP.如果
将∠BAC沿AP对折.你发现∠BAP与∠CAP重合码?由此你
能得出什么结论?





角平分线的判定:
角的内部到角的两边的距离
相等的点在角的平分线上.

l2

l1

P


角平分线的判定:
角的内部到角的两边的距离相等的点在角
的平分线上.

你能用所学的知识加以推理说明吗?

尺规作角的平分线
已知:
求作: ∠AOB的平分线.
A
B




画法:
1.以O为圆心,适当
长为半径作弧,交OA于M,
交OB于N.
2.分别以M,N为
圆心.大于 1/2MN的长
为半径作弧.两弧在∠A
OB的内部交于C.
3.作射线OC.
射线OC即为所求.






∠AOB

思考:
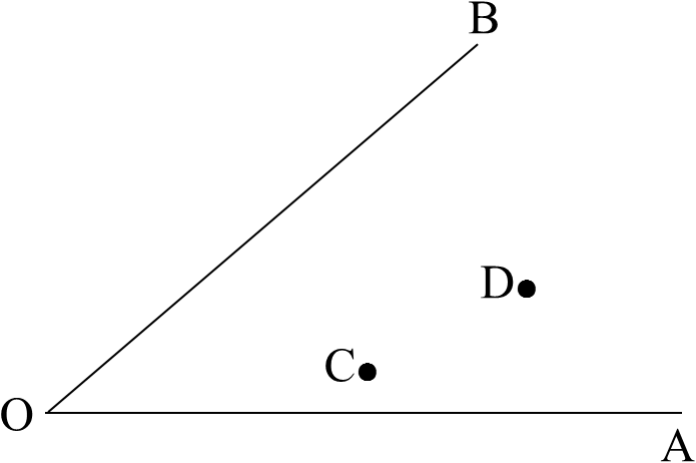
如图,求作一点P,使PC=PD,并且点P到∠AOB的
两边的距离相等.

一填空:
(1).∵∠1= ∠2,DC⊥AC, DE⊥AB
∴___________
(___________________________________________)
(2).∵DC⊥AC ,DE⊥AB ,DC=DE
∴__________
(_ ______________________________________________)
∠1= ∠2
DC=DE
到角的两边的距离相等的点,在角平分线上。
角平分线上的点到角的两边的距离相等



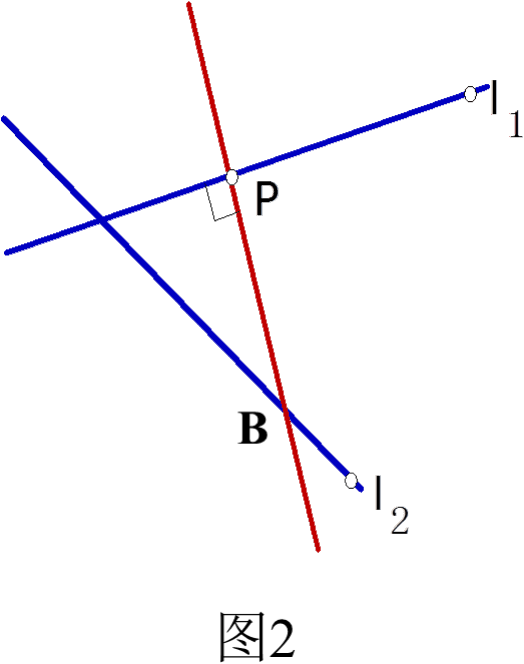
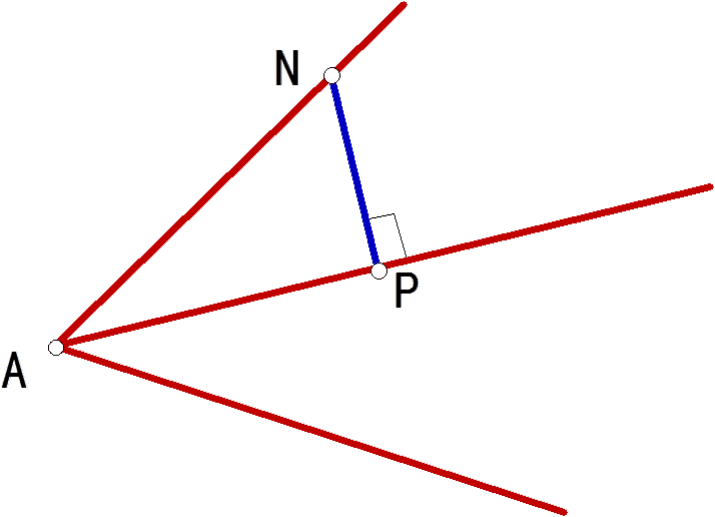
1:下列两图中,能表示直线l1上一点P到直线l2
的距离的是()

二 选择题:

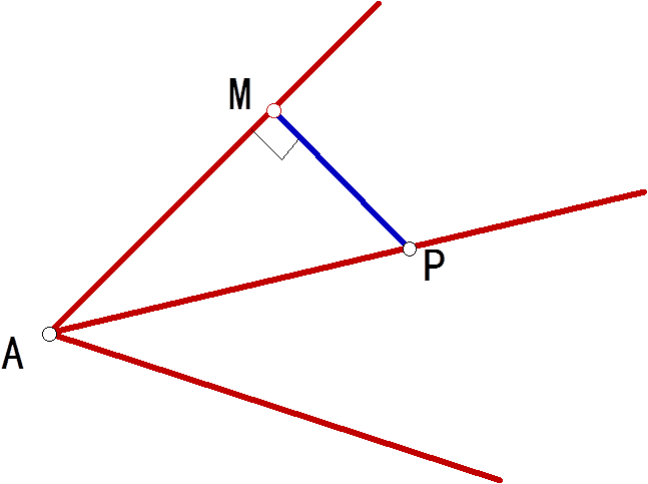
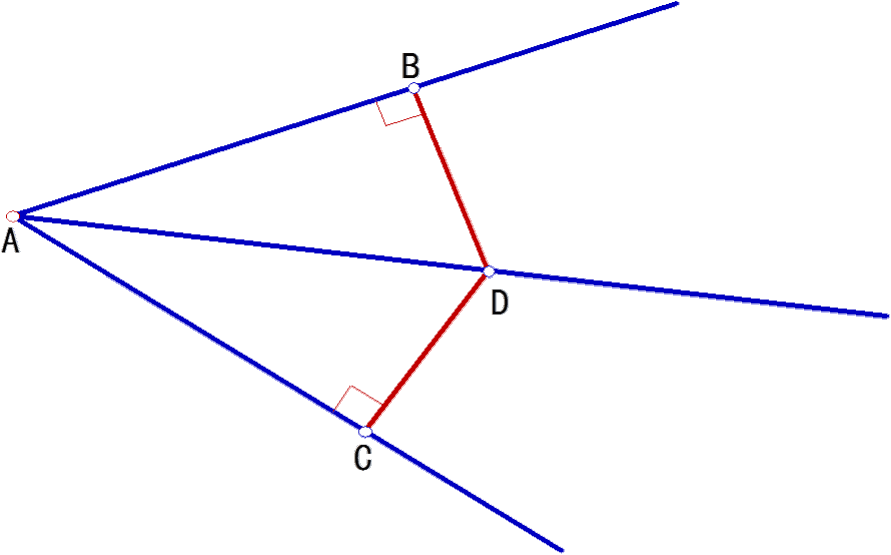
2:下列两图中,能表示角的平分线上的一点P
到角的边上的距离的是()


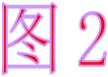

∵ 如图,AD平分∠BAC(已知)
∴=,()
角的平分线上的点到角的
两边的距离相等。
BDCD
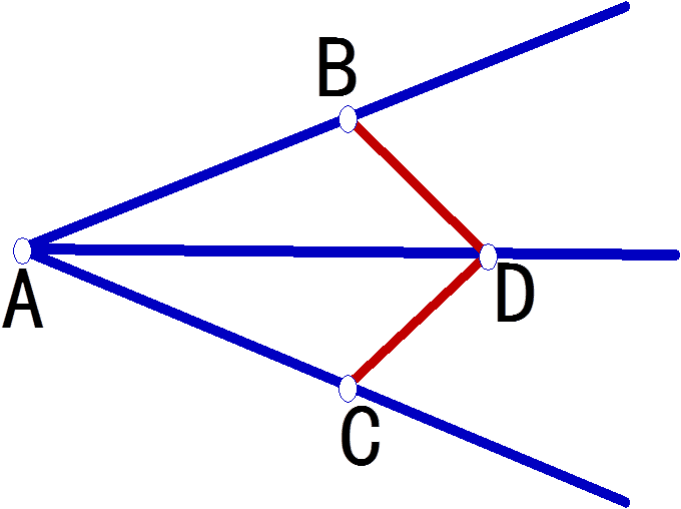
三判断:
(×)



∵ 如图, DC⊥AC,DB⊥AB(已知)
角的平分线上的点到角的
两边的距离相等。
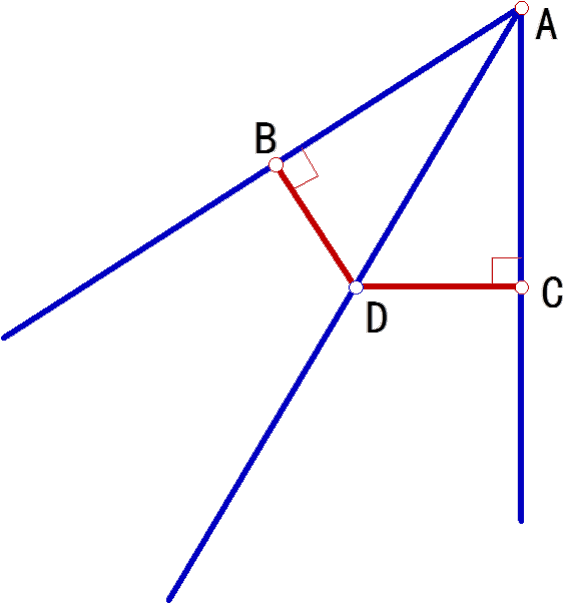
BDCD
(×)
∴=,()



∵ AD平分∠BAC, DC⊥AC,DE⊥AB(已知)
∴=,()

角的平分线上的点到角的两
边的距离相等。
√




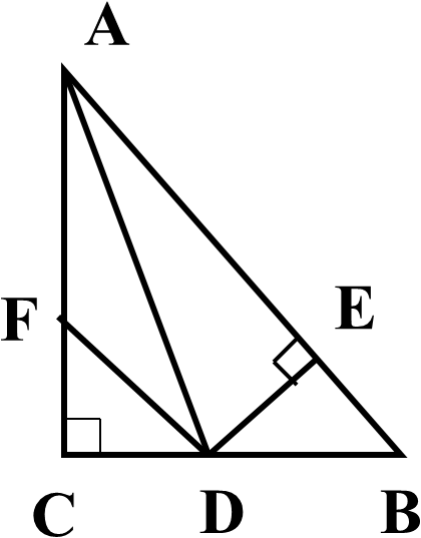
例:如图, △ABC的角平分线BM,CN相交于点P,
请问:点P在∠BAC的角平分线上吗?为什么?
A
P



M
N
B
C

结论:三角形的三条角平分线相交于一点,它到三边
的距离相等。

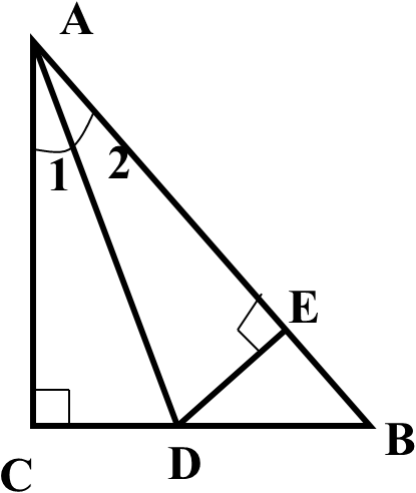
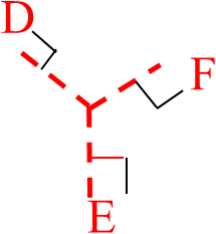
如图:在△ABC中,∠C=90° AD是
∠BAC的平分线,DE⊥AB于E,F在
AC上,BD=DF;
求证:CF=EB




四.问答

∵AD是角平分线,D在AD上,且CD⊥AC,DE⊥AB

∴CD=DE

∴可证得△FCD≌ △BED,∴CF=EB

分析:

应用于实际生活
如图,为了促进当地旅游发展,某地要在三条公路围
成的一块平地上修建一个度假村.要使这个度假村到三
条公路的距离相等,应在何处修建?
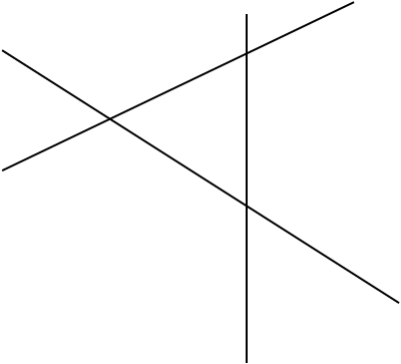
应建于三个角的
角平分线交点上

性质 角平分线上的点到这个角的
两边距离相等.
判定角的内部到角的两边的距
离相等的点在角的平分线上.
用尺规作角的平分线.



谢谢
